Konwersja liczb binarnych do kodu BCD (AVR)

Na forum elektrody natrafiłem na temat związany z operowaniem na dużych liczbach na małych mikrokontrolerach AVR. W istocie temat dotyczył algorytmu szybkiej konwersji dużych liczb zapisanych w naturalnym systemie dwójkowym na ich reprezentację w kodzie BCD. Zagadnienie to wydało mi się na tyle ciekawe i praktyczne (w kilku projektach będę przechodził podobny problem), związane też jest to pokrótce z multipleksowaniem 7-segmentowych wyświetlaczy LED, dlatego postanowiłem zrobić kilka testów (porównań) różnych algorytmów. I być może napisać jakąś własną wersję.

Jakby nie patrzeć zapis BCD można potraktować jako rozbicie liczby na jej poszczególne cyfry dziesiętne, kodowane w systemie binarnym. Taka swoista mieszanka dziesiętno-binarna, czyli system dziesiętny zakodowany dwójkowo. Stąd wzięła się nazwa tego formatu zapis liczb - Binary-Coded Decimal. Istnieje wiele różnych algorytmów umożliwiających konwersję zapisu liczb dwójkowych do reprezentacji w systemie BCD.

Intro

Na potrzeby moich eksperymentów, wszystkie testowe algorytmy zapisałem w C++ w formie generycznej, aby prosto przetestować ich działanie dla różnych typów, przy jak najmniejszym pisaniu i powtarzaniu kodu. Dzięki czemu są również dobrym kandydatem do jakiejś biblioteki algorytmów generycznych.

Dlatego wszystkie funkcje konwersujące liczby w naturalnym zapisie binarnym do kodu BCD powinny być zgodne z poniższym prototypem:

template<typename T>
void BinToBCD(T n, uint8_t* digits, size_t count);

Jako że chcę tylko używać tej funkcji do typów całkowitoliczbowych (a dokładniej integral type bez bool-a), dobrze jest skorzystać z SFINAE, aby dla innych typów zablokować kompilację:

template<typename T, typename = std::enable_if_t<
	std::is_integral_v<T> && !std::is_same_v<T, bool>
>>
void BinToBCD(...)

Ostatecznie z powodu zubożonych środowisk programistycznych C++ dla mikrokontrolerów, ograniczyłem testy tylko do typów bez znaku (unsigned): uint8_t, uint16_t i uint32_t.

Tak to prawda, środowisko C++ poza wielkimi PC-tami to w większości jakaś kpina i żart, są on totalnie nieprzyjazne, gdy chce się napisać coś bardziej sensownego niż proste konstrukcje, jak chociażby z wykorzystaniem metaprogramowania:

twitter.com/malcompl/status/856788824348909568

Dlatego taki ładny i prosty traits dla typów numerycznych:

template<typename T>
struct IntegralTraits {

	using UnsignedType = typename std::make_unsigned<T>::type;

	static constexpr T Min = std::numeric_limits<UnsignedType>::min();
	static constexpr T Max = std::numeric_limits<UnsignedType>::max();

	static constexpr T Bits = std::numeric_limits<UnsignedType>::digits;
	static constexpr T Digits = std::numeric_limits<UnsignedType>::digits10 + 1;

	using BiggerType = typename boost::uint_t<Bits + 1>::least;

};

Trzeba jakoś przekonwertować bez używania standardowych bebechów. Nawet udało mi się to bardzo prosto zrobić, ale dla uniknięcia komplikacji oraz klepania dużych fragmentów kodu i template-ów, poprawny on jest tylko dla typów unsigned. Szczegóły w kodzie źródłowym.

Wszelkie pomiary jakie można znaleźć w dalszej części tego wpisu, dokonałem na fizycznym mikrokontrolerze Atmega16A za pomocą mojego tool-a do pomiarów cykli: AVR-Tick-Counter. A używane dane to szereg kolejnych rosnących wartości liczbowych od 0 do Max danego typu:

[ 0, Max<T>/16, Max<T>/8, Max<T>/4, Max<T>/2, Max<T> ]

Co ostatecznie przełożyło się na następujące wartości liczbowe:

Test data:
  uint8_t       0       15      31      63      127     255
  uint16_t      0       4095    8191    16383   32767   65535
  uint32_t      0       268435455       536870911       1073741823      2147483647      4294967295

Kod do pomiarów kompilowany za pomocą avr-g++ w wersji 5.4.0 (Toolchain_3.6.0_1734) wydobytego z ostatniego wydania Atmel Studio, bo ostatnia samodzielna wersja toolchaina jest jakaś przedpotopowa, z nikłym wsparciem nadchodzącego standardu C++. Użyty stopień optymalizacji to O2, próbowałem też z Os, ale jakoś wychodziły o kilka cykli gorzej, zbytnio nie wnikałem w temat.

Pora przejść kolejno do implementacji i wyników pomiarów ;)

Proste dzielenie/modulo

Najprostszym sposobem jest sukcesywne dzielenie zwykłe i modulo liczby, ekstraktując poszczególne jej cyfry. Taki algorytm można bardzo prosto zapisać w postaci kilku linijek generycznego kodu w C++.

template<typename T>
void NativeDivBCD(T num, uint8_t* digits, size_t count) {

	for (size_t i = 0; i < count; i++) {
 
		digits[i] = num % 10;
		num /= 10;
	}
}

Wszystko fajnie, dopóki architektura której używamy wspiera sprzętowe operacje dzielenia. Nieszczęsny AVR nie posiada w swoim wewnętrznym ALU wsparcia dla dzielenia, a szkoda bo inne operacje arytmetyczno-logiczne są przez niego wykonywane w czasie jednego cyklu zegara.

Programowy algorytm zaszyty w libc, mimo że jest dobrze napisany, to jednak trochę cykli procesor musi skonsumować, aby wykonać dzielenie. Poniżej porównanie wykonania dzielenia względem mnożenia (w postaci errorbars), co może być zbliżone do porównania programowego dzielenia względem sprzętowego, gdyby ALU takie wsparcie posiadało.

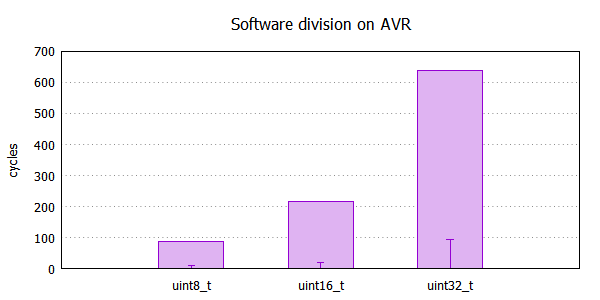
Początkowo planowałem tutaj zamieści trochę ciekawych informacji o programowym dzieleniu pod AVR-em, ale trochę się to rozrosło, idealnie nadaje się to na temat innych eksperymentów, może następnym razem ;)

Czas wykonania tego algorytmu prezentuje się następująco:

NativeDivBCD:
  uint8_t       80      80      80      80      80      80
  uint16_t      313     313     313     313     313     313
  uint32_t      5896    6058    6073    6088    6097    6109

Dla porównania, czas wykonania tego samego kodu, gdyby ALU wspierało operacje dzielenia:

HardwareDivBCD:
  uint8_t       70      70      70      70      70      70
  uint16_t      125     125     125     125     125     125
  uint32_t      637     637     637     637     637     637

Taką aproksymację sprzętowego dzielenia, tylko na potrzeby pomiarów, łatwo wykonać korzystając z mnożenia. Obie te instrukcje wymagają podobnych działań przy operacjach na typach większych niż natywne 1-bajtowce, więc otrzymane wyniki powinny być bardzo realne.

template<template<typename> class F, typename T>
void DivideBCD(T n, uint8_t* digits, size_t count) {

	for (size_t i = 0; i < count; i++)
		n = F<T>::div10(n, digits[i]);

}

// Emulate hardware ALU div by mul for approximation.
// It's only for calc used cycles when ALU has hardware div!
template<typename T>
struct HardwareDiv {

	static T div10(T n, uint8_t& r) {
		r = n * 10;
		return n * r;
	}

};

template<typename T>
inline void HardwareDivBCD(T n, uint8_t* digits, size_t count) {
	return DivideBCD<HardwareDiv, T>(n, digits, count);
}

Przy okazji rozbiłem ten generyczny kod, aby można było używać funktorów z różnymi implementacjami dzielenia przez 10. Bo w większości tutaj prezentowanych algorytmów będę zastępował dzielenie innymi operacjami arytmetycznymi lub jakimiś przekształceniami.

Nim pobawię się podmianą dzielenia na inną implementację, chciałbym zerknąć na kilka innych popularnych algorytmy i metod konwersji liczb binarnych na ich postać zapisaną w kodzie BCD.

Brute Force

Szkolnym przykładem zamiany kodu binarnego na BCD jest skorzystanie z cyklicznego odejmowania poszczególnych części dziesiętnych wraz z ich zliczeniem. Podobnie można postępować przy naiwnej implementacji operacji dzielenia. Często używaną nazwą dla tej metody jest “brute-force”.

Do generycznego zapisania tego algorytmu w języku C++, bez użycia mnożenia i dzielenia, wymagana jest tablica przeglądowa (look-up table) poszczególnych wag dziesiętnych:

static const uint32_t SubVal[] = {
	1,
	10,
	100,
	1000,
	10000,
	100000,
	1000000,
	10000000,
	100000000,
	1000000000,
};

constexpr uint32_t SubValSize = sizeof(SubVal) / sizeof(SubVal[0]);
static_assert(SubValSize == Digits<uint32_t>, "incorrect SubVal content for uint32_t");

Mając tak przygotowane niezbędne składniki, implementacja algorytmu dla dowolnych typów liczbowych staje się banalnie prosta:

template<typename T>
void BruteForceBCD(T n, uint8_t* digits, size_t count) {

	count = ::min<size_t>(count, Digits<uint32_t>);

	for (size_t i = count - 1; i > 0; i--) {

		uint8_t& dig = digits[i];
		const T& sub = SubVal[i];

		dig = 0;
		while (n >= sub) {
			n -= sub;
			dig += 1;
		}
	}

	digits[0] = static_cast<uint8_t>(n);
}

Jest to taki standardowy i najprostszy zapis tej metody, ale nie jedyny. Kilka ciekawych wariantów i modyfikacji implementacji tego sposobu można znaleźć na stronie projektu DE248 Drive Electronics w części poświęconej konwersji BCD: [Brute Force Conversion](www.dragonwins.com/domains/getteched/de248/bin2bcd.htm#Brute Force Conversion).

Otrzymane wyniki są zaskakujące:

BruteForceBCD:
  uint8_t       64      70      80      95      81      101
  uint16_t      106     199     235     236     236     243
  uint32_t      253     750     774     698     778     947

Sam byłem pewny, że wykonanie takiego algorytmu zajmie trochę więcej czasu, a tutaj taka niespodzianki. Jak się później okaże, jest to jeden z najlepszych wyników. Kto by pomyślał…

Double-Dabble (Shift and Add-3)

Jest to bardzo popularna metoda, często można spotkać ją w różnych materiałach w sieci, szczególnie przy implementacjach sprzętowego konwertera w FPGA lub innych układach programowalnych. Idea jest prosta: przesuwamy w lewo po 1 bicie konwertowaną liczbę pakując wysuwany bit w szereg kolejnych pozycji BCD. Jeśli w każdej iteracji wartość w kolumnie (danym miejscu dziesiętnym) jest większe lub równe 5 to zwiększamy wartość tej liczby o 3. I tak dalej…

Szczegóły można znaleźć w artykule na Wikipedii, a wpisując w wyszukiwarkę frazę z nazwą algorytmu znaleźć można obszerne materiały i graficzne przedstawienie poszczególnych kroków, bardzo ułatwiających zrozumienie i ideę.

Zapisanie tego w kawałku kodu C++ jest trochę upierdliwe. Idealnie tutaj nadawałby się typ 4-bitowy lub jakiś packed BCD. A że przyjąłem jako output niepakowane BCD, czyli bajt na cyfrę, to sprawa trochę się komplikuje. Musiałbym się trochę napisać, aby to ładnie zaimplementować, dlatego chwilowo wstrzymuje się z testowaniem tego sposobu. Zdecydowałem się jednak w wolnej chwili zmodyfikować załączoną na Wikipedii implementację, dostosowując ją do wymagań testowych. Oto co mi z tego wyszło:

template<typename T>
void DoubleDabbleBCD(T n, uint8_t* digits, size_t count) {

	count = ::min<size_t>(count, Digits<uint32_t>);
	size_t smax = count > 2 ? 2 : 0;	// speed optimization

	for (size_t i = 0; i < count; ++i)
		digits[i] = 0;

	for (size_t i = Bits<T>; i > 0; --i) {

		// This bit will be shifted in on the right.
		int shifted_in = (n & (1 << (i - 1))) ? 1 : 0;
		
		// Add 3 everywhere that digits[k] >= 5.
		for (size_t j = 0; j < count; ++j)
			digits[j] += (digits[j] >= 5) ? 3 : 0;

		// Shift digits to the left by one position.
		if (digits[smax] >= 8 && smax < count)
			smax += 1;
		for (size_t j = count - 1; j > 0; --j) {
			digits[j] <<= 1;
			digits[j] &= 0xF;
			digits[j] |= (digits[j - 1] >= 8);
		}

		// Shift in the new bit from arr.
		digits[0] <<= 1;
		digits[0] &= 0xF;
		digits[0] |= shifted_in;
	}

}

W sumie, funkcję tą łatwo można przerobić na uniwersalną run-time-ową formę, bo akurat implementacja szablonowa tutaj za dużo nie wnosi, ciężko cokolwiek rozwinąć lub zoptymalizować w czasie kompilacji.

DoubleDabbleBCD:
  uint8_t       1091    1091    1091    1091    1091    1091
  uint16_t      3492    3492    3492    3492    3492    3492
  uint32_t      13426   13426   13426   13426   13426   13426

Raczej szału co do szybkości to i tak nie będzie ma. Biorąc pod uwagę, że należałoby iterować w pętli tyle razy ile bitów w liczbie, a przy każdej iteracji przesuwać wszystkie pozycje dziesiętne i sprawdzać czy nie należy dodać 3-ki… Robi się to ciężkie i wolne.

Reciprocal Multiplication

Mnożenie wzajemne jest jedną z ciekawych i wydajnych metod zastępowania operacji dzielenia za pomocą mnożenia, a dalej mnożenia i dzielenia poprzez odpowiednie przesunięcia bitowe. Może to być przydatne w przypadku platform bez sprzętowych instrukcji tego typu. Bardzo dobrym materiałem źródłowym jest artykuł Jones on reciprocal multiplication.

Po krótce cała idea sprowadza się do prostych zależności arytmetycznych i aproksymacji. Dla przykładu dzielenie liczby 16-bitowej przez 10, można zapisać w takiej postaci:

$$x/10 = (x* (1/10) * 65535) / 65335 = (x * 0x1999) » 16$$

Szczegóły teoretyczne można znaleźć w powyższym materiale, na forum również kilka osób zaproponowało takie operacje, wraz z przykładami.

Takie tricki wydają się bardzo dobrym sposobem pozbycia się dzielenia, więc je przetestowałem w dwóch wersjach - jedna standardowa na mnożeniu, a druga z dodatkową zamianą mnożenia na przesunięcia bitowe z aproksymacją.

Standardowa wersja tego algorytmu z mnożeniem:

template<typename T>
struct ApproxMul {

	static T div10(T n, uint8_t& r) {

		using Trait = IntegralTraits<T>;
		constexpr T Trunc = Trait::Max / 10;

		typename Trait::BiggerType x = n;
		T q = (x * Trunc) >> Trait::Bits;

		r = n - 10 * q;
		if (r >= 10) {
			q += 1;
			r -= 10;
		}

		return q;
	}

};

Ilość pochłoniętych cykli procesora przez konwersje do BCD:

ApproxMulBCD:
  uint8_t       92      92      92      92      92      94
  uint16_t      277     280     277     277     277     280
  uint32_t      2921    2922    2927    2927    2921    2928

Wersja ta wydaje się najlepszą implementacją, mimo iż wymaga operowania na 2-krotnie większych typach liczbowych niż docelowe (uint16 * uin16 = uint32), ale gdy istnieje sprzętowe mnożenie nie wprowadza to większego kosztu.

Dla przykładu, wersja bez mnożenia, z wykorzystaniem przesunięć bitowych:

template<typename T>
struct ApproxShift {

	static T div10(T n, uint8_t& r) {
		
		using Trait = IntegralTraits<T>;
		
		typename Trait::BiggerType x = n;
		x = ((x >> 1) + x) >> 1;

	//	for (size_t i = 4; i <= Trait::Bits / 2; i <<= 1)
	//		x = ((x >> i) + x);

		// unrooling in compile-time
		x = shift_for<Trait::Bits / 2, 2>::iterate(x);

		x = x >> 3;
		T q = static_cast<T>(x);

		r = ((q << 2) + q) << 1;	// 10 * q
		r = n - r;					// r = n - 10 * q
		if (r >= 10) {
			q += 1;
			r -= 10;
		}

		return q;
	}

};

Dla pozbycia się pętli z kolejnymi przesunięciami w czasie wykonania, postanowiłem zaimplementować prostą pętle szablonową, aby kompilator w czasie kompilacji ładnie ja rozwinął do poszczególnych elementów. Niestety taki unrolling trzeba było ręcznie zapisać, więc ograniczyłem się do dedykowanego rozwiązania zapisanego na szybko, czyli coś pokroju:

template<size_t Bits, size_t End = 0, bool stop = Bits == End>
struct shift_for {
	template<typename V>
	static V iterate(V q) {
		V x = shift_for<Bits / 2, End>::iterate(q);
		return (x >> Bits) + x;
	}
};

template<size_t Bits, size_t End>
struct shift_for<Bits, End, true> {
	template<typename V>
	static V iterate(V q) {
		return q;
	}
};

Całość ładnie się rozwija w czasie kompilacji, tak jakby ktoś ręcznie zapisał poszczególne kroki.

ApproxShiftBCD:
  uint8_t       152     152     152     152     152     152
  uint16_t      578     581     584     578     578     578
  uint32_t      4194    4194    4215    4222    4201    4194

Pomiar pokazał zdecydowanie słabe wyniki, w porównaniu do wersji z mnożeniem. Nie ma co się dziwić skoro operacje przesunięć bitowych pod AVR-em są jedno-cykliczne, mogą jednym ruchem przesunąć tylko o jedna pozycję, więc większe przesunięcia wykonywane są w pętli, a każda iteracja i wykonanie shift-a kosztuje kolejne cykle.

Outro

Na koniec pozostało zbiorcze porównanie otrzymanych wyników. Jakoż, że niektóre algorytmy dla różnych wartości danego typu dawały różne wyniki (rosnące pożeranie cykli wraz z rosnącą wartością) to zdecydowałem się tutaj porównać średnie wartości wykorzystanych cykli procesora dla każdego typu. Jako benchmark, można zastosować wyniki z algorytmu pseudo-ALU (HardwareDiv) ukazującego czas wykonania w sytuacji idealnej, czyli sprzętowego dzielenia.

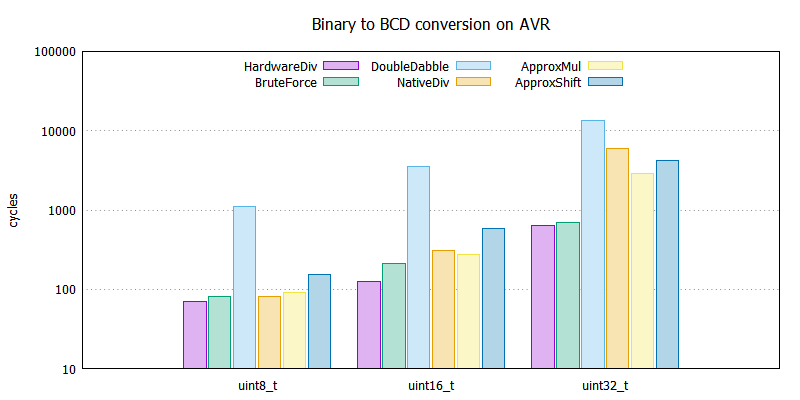
Nie ukrywam, że wyniki mnie zaskoczyły, nie spodziewałem się takiego obrotu sprawy. Uwaga, wykres posiada skalę logarytmiczną, więc wydaje się na pierwszy rzut oka, że większość algorytmów ma podobną złożoność czasową, a w rzeczywistości nie jest tak fajnie.

Sądziłem, że faworytem tutaj będzie ApproxMul i zdeklasuję konkurencję szybkością, a metoda bazująca na odejmowaniu - BruteForce będzie średnia i nie uplasuje się tak wysoko. A jednak! Dlatego warto przyjrzeć się bliżej wynikom tego algorytmu.

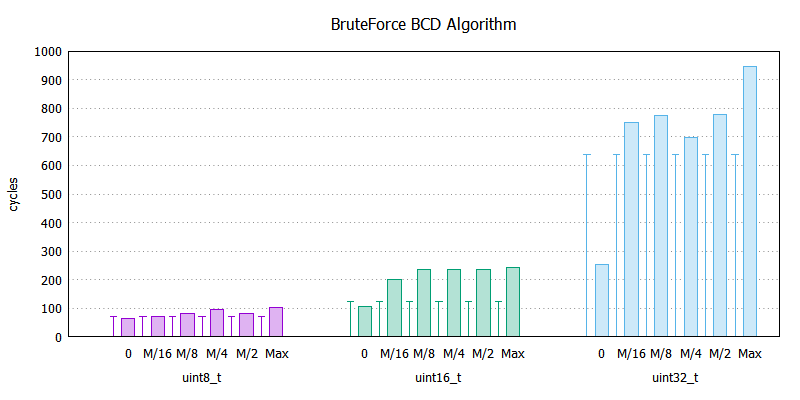
Widać wyraźnie, że utrzymuje on w miarę stały narzut względem operacji opartych na hipotetycznym sprzętowym dzieleniu w ALU (errorbars). Dobrze byłoby przeprowadzić pomiary dla większego zakresu losowych liczb, aby wyznaczyć jakaś charakterystykę.

To uświadamia mnie, że warto robić różne testy i eksperymenty, bo nie zawsze to co się wydaje będzie odzwierciedleniem rzeczywistości. Rzeczywistość lubi często zaskakiwać.

Początkowo myślałem, że wykres dla każdego algorytmu będzie się ładnie prezentował, ale jak widać prawie wszystkie algorytmy mają podobną złożoność czasową dla różnych wartości danego typu, więc finalnie pozostałem przy surowych danych wyplutych przez atmegę.

…

Kod w całości wrzucę wkrótce~~ wrzuciłem na gista, później może i przeniosę do pełnoprawnego repozytorium na githubie, gdyby zaszła taka potrzeba - na przykład przy dodaniu nowych algorytmów, modyfikacjach czy aktualizacjach…

Cała implementacja algorytmów znajduje się w pliku [bcd.h](https://gist.github.com/malcom/e425312ead749853819fe5ddfe74bad4#file-bcd-h). Implementacja benchmarku dla AVR w pliku [avr.cpp](http://gist.github.com/malcom/e425312ead749853819fe5ddfe74bad4#file-avr-cpp). Kod zawiera także testy jednostkowe bazujące na Boost.Test (plik [test.cpp](http://gist.github.com/malcom/e425312ead749853819fe5ddfe74bad4#file-test-cpp), które można skompilować pod komputerem i zweryfikować poprawność działania algorytmów. Przydatne do dalszych eksperymentów, modyfikacji czy innych zabaw ;)

…

Jak wspomniałem na początku, kod ten można wykorzystać we własnej bibliotece lub używać bezpośrednio z nagłówka bdc.h. Użycie zamieszczonych funkcji jest bajecznie proste:

uint32_t n = ...

uint8_t bcd[Digits<uint32_t>];
BruteForceBCD(n, bcd, sizeof(bcd));

Dzięki traitsom łatwo można rezerwować na stercie tablicę na potrzeby wyników, o rozmiarze pozwalającym pomieścić wszystkie pozycje dziesiętne danego typu liczbowego.

Funkcje do konwersji binary to BCD mogą też być wykorzystane przy konwersji liczb na stringi. Wystarczy dodać odpowiedni offset ('0') do każdego bajta, aby otrzymać poprawne znaki ASCII.

…

Większość kodów została napisana w jak najprostszej postaci. Choć dla programistów niezaznajomionych z językiem C++ i jego idiomami niektóre template-owe fragmenty mogą wyglądać jak potworki, to mówiąc szczerze gorzej mogłoby być przy babraniu się pod prawie 15-letnim C++03 ;) Niektóre algorytmy można byłoby jeszcze nieco zoptymalizować. Najprostszym sposobem dla wszystkich metod bazujących na DivideBCD jest pomijanie operacji dzielenia lub całkowite przerwanie, gdy w wyniku poprzedniej operacji otrzymamy 0.

	for (size_t i = 0; i < count; i++) {
		if (n > 0)
			n = F<T>::div10(n, digits[i]);
		else
			digits[i] = 0;
	}

W takiej sytuacji nie ma sensu już dalej iterować, można za to do końca tabeli wynikowej wpakować zera, albo zwracać rozmiar wypełnionych danych… Ciekaw jestem jak w takiej sytuacji zmienia się aktualne wyniki. Ciekaw jestem jak w takiej sytuacji aktulane wyniki mogły by się zmienić.

Całkiem możliwe, że przedstawiony materiał doczeka się aktualizacji lub kontynuacji. Być może ktoś zaproponuje jakiś dodatkowy algorytm do przetestowania, albo sensowne optymalizacje. Choć dla wersji BruteForce-a chyba nie ma już zbytnio możliwej poprawy.

Na koniec zachęcam do zajrzenia na wspomniany temat na forum elektrody, gdzie może toczyć się również ciekawa dyskusja odnośnie tej tematyki.