Metodyka wyceny portfela

Jednym z kluczowych problemów dotyczących inwestowania jest pomiar i ocena wyników zarządzania portfelem inwestycji. Pierwszym i najbardziej popularnym sposobem jest wyznaczenie stopy zwrotu i porównanie jej do benchmarku. O ile wyznaczenie stopy zwrotu ze stałych, czy jednorazowych inwestycji jest sprawą prostą, to problemem może być określenie stopy zwrotu z portfela, w którym ciągle coś się dzieje, występują różne przepływy pieniężne.

Odkąd zacząłem inwestować na giełdzie, mój portfel został podzielony na cześć pasywną/bezpieczną i aktywną/agresywną/ryzykowną - czyli obecnie akcyjną, gdzie cała zawartość inwestowana jest w akcje, zacząłem szukać prostej metody pozwalającej wycenić moje zarządzanie i podejmowane decyzje inwestycyjne. Szczególnie, że część akcyjna, dalej zwana portfelem, podobnie jak pozostałe części ciągle rośnie, a wiec zainwestowany kapitał zmienia się w czasie.

Jako, że nie jestem ekonomistą, chciałem pominąć cały ten teoretyczny bełkot ekonomiczno-matematyczny, i wszelkie długie wzory, wyglądające, na pierwszy rzut oka, na skomplikowane i skupić się na konkretach. Chociaż z wzorami to nie mam najmniejszych problemów, ale po co zaśmiecać sobie tym głowę, szczególnie, gdy potrzebujemy prostej i zrozumiałej dla wszystkich metodyki.

Prosta stopa zwrotu

Ogólny zysk z inwestycji, mógłbym potraktować jako inwestycję prostą, i wyznaczyć jej stopę zwrotu R za pomocą standardowego i ogólnie znanego wzoru, opartego na stosunku wartości kapitału K w rozpatrywanym czasie:

$$R_t=\frac{K_{t}}{K_{t-1}}-1$$

co w bardziej prostszej formie można zapisać w postaci:

$$R_t=\frac{K_{t}-K_{t-1}}{K_{t-1}}$$

lub w przypadku inwestycji w akcje uwzględnić wypłacone dywidendy D:

$$R_t=\frac{(K_{t}-K_{t-1})+D_{t}}{K_{t-1}}$$

Wynikiem obliczeń z zastosowaniem przedstawionych wzorów będzie stopa zwrotu z całości inwestycji, biorąc jako kapitał sumę wszystkich poszczególnych dopłat kapitału inwestycyjnego. Jest to przydatna informacja, bo dowiem się ile realnie zarobiłem na inwestycjach, wystawiając na ryzyko zaangażowane w to pieniądze. Niestety będzie to ściśle związane z wartością kapitału i jego zmianą w czasie.

Mając w portfelu kilka akcji, mógłbym stopę zwrotu wyznaczać na podstawie udziału (procentowo-wartościowego lub ilościowego) x poszczególnych walorów portfela, korzystając z następującego wzoru:

$$R_p=(R_1x_1)+(R_2x_2)+…+(R_n*x_n)$$

Widzimy, że stopa zwrotu portfela odpowiada sumie ważonej stóp zwrotu R poszczególnych walorów, przy czym wagami x są udziały tych walorów w portfelu:

$$R_p=\sum_{i=1}^NR_ix_i$$

I to miałoby sens, gdyby każda kolejna inwestycja w portfel była równomiernie rozkładana na poszczególne aktywa portfela, zgodnie z ich udziałami. A ja wiem, że tak łatwo i prosto nie będzie. Nowy kapitał dopływający do portfela, może być rozdysponowany na całkiem nowe aktywa. I tutaj dochodzimy do sedna istoty problemu.

Stopa zwrotu z przepływami

Moje pomiary stopy zwrotu portfela silnie związane są z wpływami i wypływami pieniężnymi oraz zmianami składu walorów wraz z ich udziałem w portfelu, które występują w rozpatrywanym okresie inwestycji. Wpływają one na wartość portfela, a tym samym na wartość stopy zwrotu, co w konsekwencji prowadzi do zaburzeń wyników, a nie powinny mieć żadnego wpływu na ocenę wyników zarządzania moimi inwestycjami.

Z podobnymi problemami borykają się wszelkie fundusze inwestycyjne, także te emerytalne. Istnieje wiele sposób poradzenia sobie z tym problemem.

Jeśli założymy, że wszelkie przepływy CP mogą pojawiać się tylko na początku (b) lub na końcu (e) rozpatrywanego okresu inwestycji, to stopę zwrotu możemy określić za pomocą następującego wzoru:

$$R=\frac{(K_e-CP_e)-(K_b+CP_b)}{(K_b+CP_b)}$$

Wzór ten może być użyteczny tylko, gdy częstotliwość występowania przepływów pieniężnych jest stosunków mała, wtedy rozpatrywane okresy są stosunkowo długie. W innych przypadkach może być nieco kłopotliwy.

Obecnie istnieją dwa rozwiązania wszelkich problemów opisanych wyżej: stopa zwrotu ważona czasem - TWR (Time Weighted Return) i stopa zwrotu ważona przepływami - MWR (Money Weighted Return). Prócz tych dwóch głównych metod, popularne są bazujące na nich inne sposoby wyznaczania stopy zwrotu: IRR - Wewnętrzna stopa zwrotu (Internal Rate of Return), XIRR (IRR dla serii rozłożonych w czasie przepływów gotówkowych, niekoniecznie okresowych), czy oparte na wewnętrznej jednostce rozrachunkowej.

Metoda TWR oraz ta oparta na wewnętrznej jednostce rozrachunkowej są najpopularniejszymi sposobami, które potrafią odpowiedzieć nam, na podstawowe pytanie o stopę zwrotu portfela w zadanym horyzoncie czasowym, z uwzględnieniem wszystkich jego zmian (wpłat i wypłat). Ta pierwsza jest uważana za standard rynkowy wśród instytucji finansowych i promowana (rekomendowana) przez rekomendowana przez CFA Institute w standardach GIPS. Druga natomiast, jest szeroko stosowana przez wszelkiego rodzaju fundusze inwestycyjne oparte na jednostkach uczestnictwa, czy certyfikatach, gdzie nie używa się TWR. Dlatego obie te metody najbardziej mnie zainteresowały.

TWR

Metoda TWR polega na łączeniu stóp zwrotu osiągniętych w okresach pomiędzy wpłatami i wypłatami środków, bazując na wyżej przedstawionym wzorze, niwelując w ten sposób wpływ wszelkich przepływów pieniężnych na całkowitą stopę zwrotu portfela w zadanym okresie:

$$R_{TWR}=(1+R_0)(1+R_1)…(1+R_n)-1$$

Nazwa tej metody odzwierciedla jej proces wyznaczania stopy zwrotu, gdzie każdy okres otrzymuje wagę proporcjonalną do długości tego okresu w relacji do długości całego okresu inwestycji.

Przy obliczaniu dziennej stopy zwrotu TWR, wagi te będą równe jedności, jak w powyższym wzorze, a dzienną stopę zwrotu można uprościć do stosunku wartość aktywów W portfela w danym czasie t skorygowaną o bilans przepływów CP do wartość portfela w dniu poprzedzającym:

$$R_t=\frac{W_t-CP_t}{W_{t-1}}$$

Jednostka rozrachunkowa

Metoda oparta na wyznaczania wewnętrznej jednostki rozrachunkowej, skupia się na wyznaczeniu wartości pomocniczej , ułatwiającej prowadzenie i rozliczanie stanu konta i stopy zwrotu inwestycji, która jest zawsze wartością księgową udziału w danych aktywach portfela lub funduszu (gdyż często wykorzystywana jest przez fundusze inwestycyjne).

Stopa zwrotu określana jest na podstawie zmian wartości danej jednostki rozrachunkowej w czasie, która w branży TFI często zwana jest jednostką uczestnictwa lub certyfikatem inwestycyjnym.

Wycena jednostek dokonywana jest w dwóch etapach. Pierwszym etapem jest wyznaczenie wartości aktywów netto całego portfela (funduszu) w dniu wyceny, co uściślając, jest wartością aktywów portfela pomniejszonych o zobowiązania i koszty. Kolejny etap ustala ostateczną wartość jednostki na dany dzień wyceny, przez podzielenie wartości aktywów netto w dniu przeliczenia przez liczbę wyemitowanych jednostek rozrachunkowych (zapisanych w tym dniu na rachunkach prowadzonych przez fundusz).

Cały ten proces można zapisać w postaci następującego wzoru:

$$J_t=\frac{W_t-C_t}{N_t}$$

Wpłaty do portfela odzwierciedlają zakup jednostek funduszu, a wypłaty ich odkupienie (umorzenie) przez fundusz. W obu tych sytuacjach, dana wartość przepływu pieniężnego przelicza się na ilość jednostek rozrachunkowych po bieżącej wycenie (zależne od funduszu) i odpowiednio powiększa lub pomniejsza aktywa portfela.

Porównanie

Do porównania obu przedstawionych metod, jakie brałem pod uwagę, wykorzystajmy fikcyjny portfel, którego skład i wartość zmieniała się w czasie, według poniższych danych:

data		przeplywy		gotowka		energa			vistal			aktywa
2014-01-02					2025,00		15,95	500						10000,00
2014-01-03					2025,00		15,90	500						 9975,00
2014-01-07					2025,00		15,80	500						 9925,00
2014-01-08	 1500,00		2049,00		15,80	500		12,25	123		11455,75
2014-01-09					2049,00		15,83	500		12,64	123		11518,72
2014-01-10	-1000,00		1049,00		15,85	500		12,60	123		10523,80
2014-01-13					1049,00		16,54	500		13,29	123		10953,67
2014-01-14					1049,00		16,49	500		13,34	123		10934,82
2014-01-15					1049,00		16,41	500		13,27	123		10886,21
2014-01-16	-5000,00		 149,00		16,45	250		13,49	123		 5920,77
2014-01-17					 149,00		16,71	250		13,75	123		 6017,75

Przykładowe wyniki dla przedstawionych danych, wyznaczone stopy zwrotu oraz poszczególne współczynniki dla każdej z metod przedstawia prezentują się poniżej:

data			JRn		JRw		JR %		TWR			TWR %
2014-01-02		100,00	100,00	 0,00%		1			 0,00%
2014-01-03		100,00	 99,75	-0,25%		0,9975		-0,25%
2014-01-07		100,00	 99,25	-0,75%		0,994987469	-0,75%
2014-01-08		115,11	 99,52	-0,48%		1,003098237	-0,44%
2014-01-09		115,11	100,06	 0,06%		1,005496803	 0,10%
2014-01-10		105,12	100,11	 0,11%		1,000441021	 0,15%
2014-01-13		105,12	104,20	 4,20%		1,040847413	 4,24%
2014-01-14		105,12	104,02	 4,02%		0,998279116	 4,06%
2014-01-15		105,12	103,56	 3,56%		0,995554568	 3,60%
2014-01-16		 56,84	104,17	 4,17%		1,003174659	 3,93%
2014-01-17		 56,84	105,87	 5,87%		1,016379626	 5,63%

Gołym okiem widać, że wyniki obu metod są do siebie zbliżone, choć w pewnych momentach różnią się nieznacznie, co łatwo zaobserwować przy graficznym zobrazowaniu wyników, w postaci wykresu liniowego:

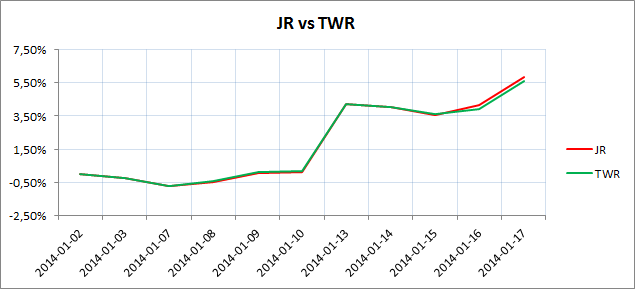
Zachodzące zmiany i dysproporcje wyników można zauważyć w okolicach występowania przepływów pieniężnych portfela. Nie są to zbyt wielkie różnice, można pokusić się o przeanalizowanie dłuższego okresu i z bardziej dynamicznymi przepływami i zmianami aktywów, aby sprawdzić, czy będą one skorelowane ze zmiennością i rozbieżnością wyników obu metod. Na pewno taka korelacja występuje przy wykorzystaniu metody MWR, o której tutaj nie mówiliśmy. Wyznaczana za jej pomocą stopa zwrotu jest ważona przepływami, a zatem jest bardzo wrażliwa na wielkość i moment ich występowania.

Ja osobiście do prezentacji, analizy stóp zwrotu i efektywności swojego portfela zacząłem używać metody opartej na jednostkach rozrachunkowych - JR, choć obecnie zastanawiam się nad przejściem na TWR. Przede wszystkim skłania mnie do tego znacznie prostszy proces wyznaczania wyceny portfela. Nie będę musiał wtedy zajmować się odpowiednim “skalowaniem” przepływów na jednostki rozrachunkowe, a jedynie skupić się na wyznaczeniu stosunku wartość aktywów w danych dniach. A zatem, głównym powodem jest wygoda oraz fakt, że TWR staje się poniekąd standardem używanym na świecie. Co wcale nie znaczy, ze wycena na podstawie jednostek rozrachunkowych jest gorsza. Ona również sprawdza się wyśmienicie, a nawet daje coś więcej od siebie - wyznaczona wartość jednostki sama w sobie daje nam jakąś istotna informację o efektywności naszych decyzji inwestycyjnych czy strategii.

Podsumowując, wyznaczenie stopy zwrotu portfela z nieco bardziej skomplikowaną strukturą wcale nie jest taką trywialną sprawą, na jaką początkowo mogłoby wyglądać. Ale po przebrnięciu pewnych aspektów i przemyśleniach, sprawa ta, również nie jest taka skomplikowana. Należy dobrze się zastanowić i skorzystać z odpowiednich środków i narzędzi, a wszystko pójdzie gładko.